This article was originally published at Imagination Technologies' website, where it is one of a series of articles. It is reprinted here with the permission of Imagination Technologies.
Firstly, I’d like to give you an overview of OpenCL programming fundamentals using a basic program, followed by an explanation of OpenCL execution on Rogue GPUs.
This provides the background to understand the programming guidelines for the Rogue architecture which are illustrated by using a case study of an image filtering program.
OpenCL overview
Consider a simple C program that multiplies the corresponding elements in two 2-dimensional arrays:
void matrix_mul_cpu(const float *a, const float *b, float *c, int l, int h)
{
int i;
for (i=0; i<l; i++)
for (j=0; j<h; j++)
c[i][j] = a[i][j] * b[i][j];
}
The for loop consists of two parts: the vector range (two dimensions containing l*h elements), and a multiplication operation. All loop iterations are independent in that there are no data-dependencies between any iterations of the loops. This means that the multiplication operations can be executed in parallel on the GPU’s numerous threads.
OpenCL programs consist of two parts: one that runs on the host CPU, the other that runs on the GPU device. To execute code on the GPU, you first define an OpenCL kernel, which is written in a variant of C with some additional keywords and data types. Continuing with the above example, an OpenCL kernel that implements a single multiplication is as follows:
_kernel void vector_mul(__global const float *a, __global const float *b, __global float *c)
{
size_t i = get_global_id(0);
size_t j = get_global_id(1);
c[i][j] = a[i][j] * b[i][j];
}
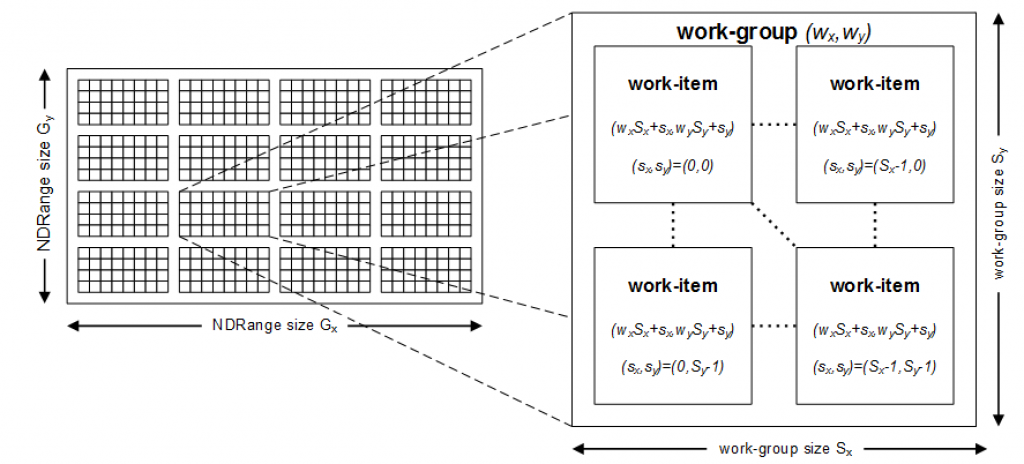
The host program launches (or enqueues) this kernel, spawning a virtual grid of concurrent work-items as illustrated below for a 2D grid of size 512 (32×16). The grid is an N-dimensional range where N=1, 2 or 3 (or NDRange). A single work-item executes for each point on the NDRange; each work-item executes the same kernel code but has a unique ID that can be queried and used to determine the data to be processed. This ID is obtained using the built-in function get_global_id.
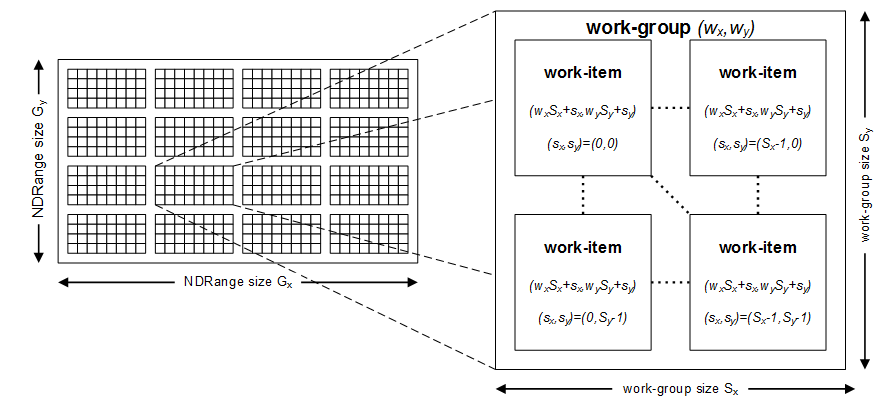
In OpenCL, multiple work-items are grouped together to form workgroups. In the figure above, each workgroup size is 8×4 comprising a total of 32 work-items. Work-items in a workgroup can synchronize with one another and share data using local memory (to be explained in a later article).
OpenCL execution on the PowerVR Rogue architecture
As shown below, from an OpenCL perspective, PowerVR GPUs are built around scalable arrays of multithreaded processors called Unified Shading Clusters (USCs). When a program running on the CPU enqueues an OpenCL kernel, all work-items in the NDRange are enumerated. The workgroup IDs and work-item IDs are enqueued sequentially in row-major order. The Coarse Grain Scheduler assembles the work-items into groups of up to 32 threads, termed warps, and streams these warps to the multiprocessors with available execution capacity. The warps containing the work-items for a complete workgroup are always allocated to a single multiprocessor.
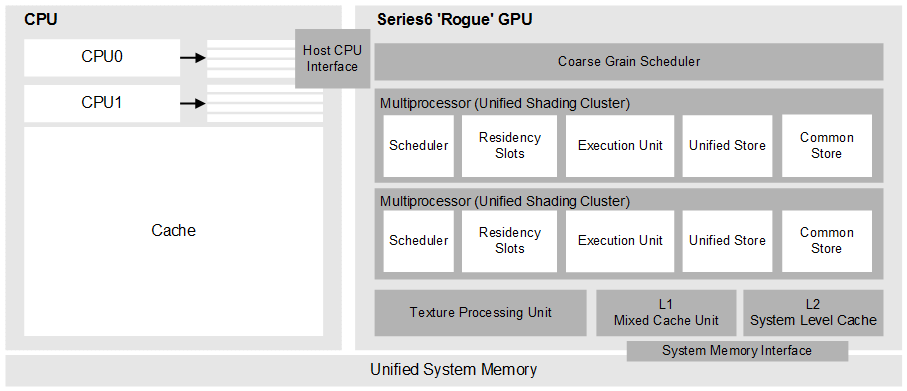
The multiprocessors execute the warps obtained from the Coarse Grain Scheduler, with the assistance of one or more Texture Processing Unit (TPU), L1 and L2 cache units. The precise number and grouping of these hardware blocks is product-specific.
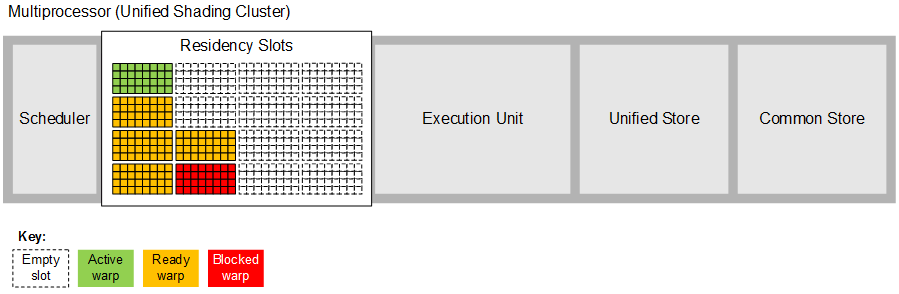
As shown below, each multiprocessor contains a number residency slots that at any time are either empty (illustrated as a grid with a dotted line) or occupied by a warp (illustrated as a grid with a solid line and colour fill). Each warp can be in one of three states: active (green fill) which means it is currently running on the execution unit; ready (orange fill) which means the scheduler may run the warp on the execution unit after executing the active warp; and blocked (red fill) which means that one or more of the work-items in the warp is awaiting a memory or barrier operation to complete. In this example, the multiprocessor has six warps to schedule: the first is active, four are ready to be executed and a single warp is blocked on a memory or barrier operation.
A multiprocessor can execute at most one warp on its execution unit at any one time. The work-items in the active warp are usually executed together in lock-step parallel as shown below, and continue executing either until completion or until the work-items become blocked on a memory or barrier operation. In this example, all 32 work-items in the active warp execute the first kernel statement together and then all progress on to the second kernel statement together.
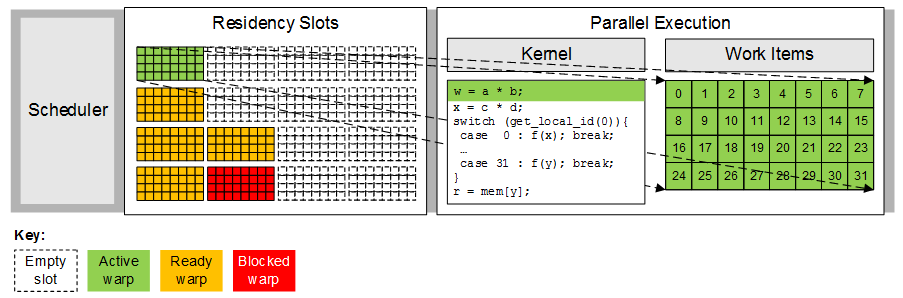
Full lock-step parallelism is achieved when all threads in a warp follow the same control path. If the threads diverge via a conditional branch, as illustrated in the figure below, the work-items stop executing together lock-step and instead the hardware serially executes each branch path taken. In this example, all work-items in the warp follow separate paths (work-item 0 executes case 0, work-item 1 executes case 1 and so on), resulting in a 32-way branch divergence. A more common scenario is an if-else statement whereby some of the work-items follow the if-statement and the other work-items follow the else-statement, resulting in a two-way divergence. In this case the compiler and hardware can minimise the impact of the divergence by using hardware predication. The compiler translates the code sequence whereby the branch condition is first calculated (true or false) and then both the if and else target instructions are executed in sequence using the branch condition as an instruction predicate. In this way, all of the instructions are executed, but only the instructions with a true predicate write results.
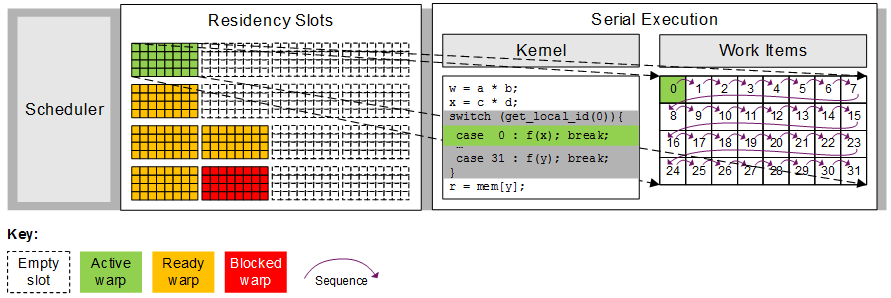
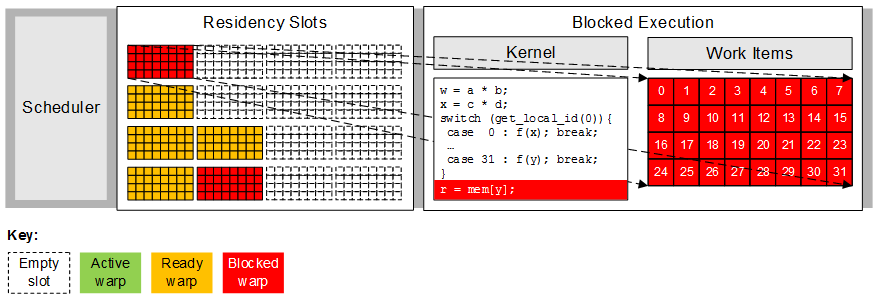
Whenever a warp is descheduled, for example due to completion, a memory or barrier operation, the multiprocessor selects another resident warp that is ready to execute. In the figure below, the first warp has reached a statement that reads from an array allocated to system memory (mem), preventing it from continuing until some point in the future when the data has been fetched; the multiprocessor is able to continue performing useful work during this time by selecting one of the other four ready warps to execute.
The execution state for each work-item (and, therefore, each warp) is maintained on-chip for the entire lifetime of the work-item in the unified store; shared local memory is held in the common-store (both shown in above). As a result, a multiprocessor can context switch between warps with zero cost. The figure below shows an example timeline for a multiprocessor scheduling between four warps. The scheduler starts executing warp 0, which runs until it reaches a blocking operation such a read or write to system memory. At this time the scheduler de-schedules warp 0 and starts executing warp 1. The work-items in all warps implement the same kernel, and therefore have similar performance characteristics, reflected in the similar (phase-adjusted) timelines in the example. At a time around half way into execution of warp 2, the operation that warp 0 was blocked on completes, so that warp 0 returns to a ready state. Later, after the scheduler has executed the first statements in warp 3, the scheduler re-schedules warp 0. The effect of this concurrent scheduling is that the impact of memory latency when processing each warp is hidden. In this scenario, the system is able to completely hide the memory latency.
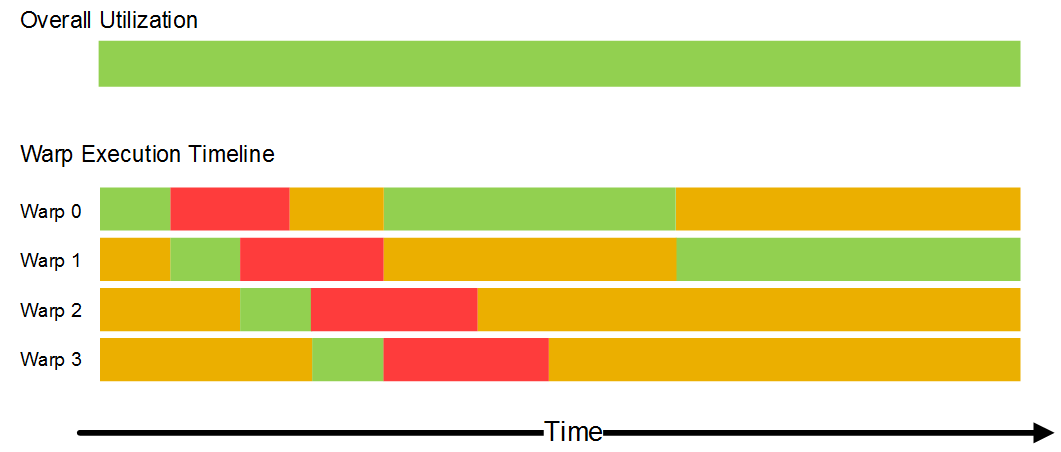
The figure below shows a similar scenario but where the round-trip-time to memory is larger. In this case, by the time warp 3 blocks on its first memory operation, warp 0, 1 and 2 are all still waiting for their memory operations to complete. All warps are therefore all blocked at the same time, with a corresponding reducing in utilization and performance.
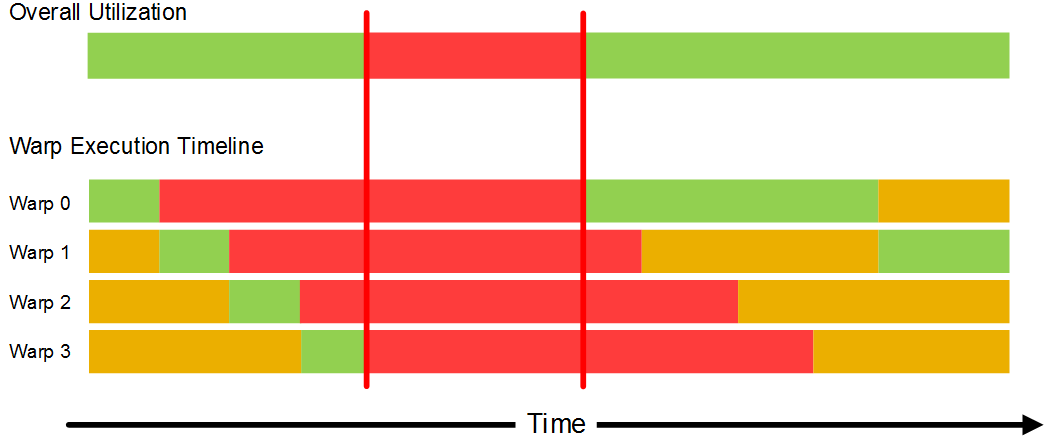
In this case, utilization could be improved if there were more than four resident warps on the multiprocessor. The total number of warps that a multiprocessor can maintain on-chip depends on factors such as the time it takes to execute each warp and the memory requirements of each warp. If a work-item allocates a large amount of private memory, the total number of work-items (and, therefore, warps) that can reside on a multiprocessor may be limited by the size of the unified store.
Similarly, if a workgroup allocates a large amount of shared local memory, the total number of workgroups that can reside on a multiprocessor may be limited by the size of the common store.
Programming guidelines
RECOMMENDATION: If possible use a workgroup size of 32.
If permitted by a kernel’s logical structuring, you are advised to use a workgroup size of 32. In this case, each warp contains a complete workgroup and all synchronization costs are free (they all happen together on the same cycle in lock-step). For larger workgroup sizes, each workgroup is implemented using multiple warps, and barrier synchronization requires the multiprocessor to perform context switches between these warps. For smaller workgroup sizes such as 4, 8 and 16, if the workgroup size is specified at compile-time, multiple workgroups are packed into a warp. For non-standard workgroup sizes, alignment restrictions on how the hardware can pack the workgroups into warps means that the warps are underpopulated with idle threads, reducing efficiency.
RECOMMENDATION: Specify your workgroup size at compile-time.
For a given kernel, you can specify the workgroup size for which it can be enqueued by specifying the following attribute.
__attribute__((reqd_work_group_size(X, Y, Z)))
The workgroup size is the product of X, Y and Z. Specifying a fixed workgroup size allows a number of additional compile-time optimizations that improve performance such as reducing the number of instructions required for barrier synchronization.
RECOMMENDATION: For image processing tasks, declare your kernel parameters as image and sampler data types (as opposed to character arrays) to benefit from TPU acceleration.
As discussed previously, the TPU provides efficient sampling of image data, image interpolation, border-pixel handling. Specifying border-pixel handling in the sampler avoids the need for special conditional code within the kernel to handle these edge conditions, reducing divergence. Using image parameters also enables your kernel to be efficiently incorporated as part of a larger heterogeneous program.
RECOMMENDATION: Use float data types inside your kernel to maximize ALU throughput.
On Rogue devices, each thread can perform floating-point operations on up to two datasets per cycle, or it can perform integer operations on a single dataset. In practice, there is usually sufficient instruction-level parallelism in the kernel code for the compiler to generate dual-issue floating-point instructions. To maximize arithmetic throughput, you should therefore perform arithmetic on float data types wherever possible.
Use the built-in function read_imagef to sample a pixel from an OpenCL image. This function uses hardware to fetch the pixel’s constituent values (either r/b/g or y/u/v values) and write these values into elements of the returned float4 vector.
RECOMMENDATION: Trade precision for speed wherever possible. Use the compiler flag
-cl-fast-relaxed-math to enable arithmetic optimizations that trade precision for speed.
Depending on the precision requirements of the application, you can often improve speed by limiting the use of arithmetic operations with long execution times.
- Use the -cl-fast-relaxed-math build option, which enables many aggressive compiler optimizations for floating-point arithmetic.
- Use native_* and half_* math built-ins, which have lower precision but are faster than their un-prefixed variants.
RECOMMENDATION: Minimize conditional code.
In general you should minimise conditional code, especially with regards to nested conditional statements. Flow control statements (if, switch, do, for, while) can reduce instruction throughput by causing threads to diverge in their execution paths requiring the hardware to serialize execution of work-items in a warp. The compiler attempts to reduce the effect of divergence using hardware predication.
RECOMMENDATION: Avoid short kernels with low arithmetic intensity.
In general, the smaller the ratio of the number of arithmetic to memory instructions (or arithmetic intensity), the higher the occupancy is required to hide the memory latency. If this ratio is 50, for example, then to hide a memory access latency of about 500 clock cycles about 10 warps are required. If the multiprocessor contains 16 residency slots, this translates to a required occupancy of around 63%.
Barrier instructions can also force the multiprocessor to idle as more and more warps wait for other warps in the same workgroup to complete execution of instructions prior to the barrier. Having multiple resident workgroups in the multiprocessor can help reduce idling in this case, as warps from different workgroups do not wait for each other at barriers. To increase the number of resident workgroups per multiprocessor, consider reducing your workgroup size.
By Doug Watt
Multimedia Strategy Manager, Imagination Technologies