This blog post was originally published at Qualcomm’s website. It is reprinted here with the permission of Qualcomm.
Combining machine learning and classical algorithms through neural augmentation for combinatorial optimization
Machine learning (ML) is transforming industries, improving products, and enhancing everyday life for consumers. You should think of ML as a horizontal technology that will impact virtually everything, like electricity or the internet.
When we hear about ML, we often hear about data. Many people think that it only makes sense to focus on ML if there are vast amounts of data available. It’s true that if there is a lot of data, ML technology will help gain new insights, automate processes, and dynamically respond to changes. A new suite of techniques known as ‘deep learning’ have become the next level of what many people know as ‘signal processing.’ Many successful companies today have made it their business model to collect data on an unprecedented scale and train models based on them featuring up to a 175 billion parameters. Training these models is quite expensive, as it has to be done with thousands of GPUs, using considerable amounts of power.
What I want to talk about in this blog post is the fact that ML can even be useful without data. When DeepMind’s AlphaGo beat the Go world champion, Lee Sedol, it had been trained on thousands of games played by Go grandmasters. However, the next versions of this piece of technology, in particular AlphaZero used zero data to be trained. It basically knew the rules of the game and subsequently played millions of games against itself. You turn your computer on at night before you go to sleep with the request to train a model on your favorite game, and the next morning it beats not only you, but every human on earth. No data necessary.
How can this technology be useful? Many problems that need to be solved are of the sort where you want to optimize some objective over a very large (and I mean larger than the number of atoms in the universe) number of possibilities. Take for example the ‘vehicle routing problem’ where you want a strategy to fill your trucks at warehouses with goods that need to be delivered to customers. Which truck should take which goods from which warehouses, take which route, and deliver to which customers? There is clearly a huge number of possibilities, many more than you can test out in a lifetime, even on a supercomputer.

Vehicle routing problem has a huge number of possibilities to exhaustively evaluate.
As another example: how do you place billions of transistors on a chip such that they meet performance criteria while minimizing the total area? Perhaps, for both problems you can appreciate that there is an analogy with playing the game of Go, where the number of possible games is also unimaginably large.
To make things worse, imagine we may need a strategy that can handle uncertainty: will the road be congested, will some truck drivers report in ill, and so on? And on top of that we may need to adapt our strategy on the fly: our current strategy may suddenly fail because some roads are blocked. It is for these types of very hard combinatorial optimization problems that a new technology is starting to emerge. The general class of methods is known as reinforcement learning (RL). AlphaGo happens to be a particular example of it. And as I argued, for some problems where you can simulate the world (like the game of Go) you do not need real data to train it.

Reinforcement learning is a ML method that allows you to train a model without real data.
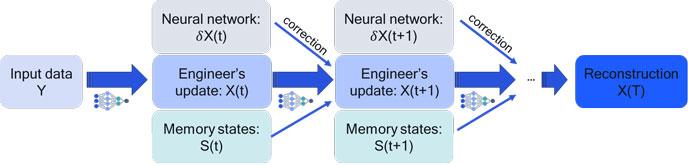
But should we throw decades of research on classical algorithms for combinatorial optimization out the window? I think not. The idea is to take your favorite classical solver and embed it into a neural network architecture. You can think of each iteration of the classical solver as a layer in a (recurrent) neural net (RNN), where the operation is fixed and not flexible. It was hand-designed by engineers over the course of decades through theory, trial, and error. But now let’s add flexible neural network operations to each layer (or iteration) with learnable parameters. The neural network can correct the classical solver depending on the particular context it is operating in. I call this ‘neural augmentation.’

Illustration of neural augmentation where a classical iterative optimization is corrected by a neural network.
This hybrid system needs much fewer parameters than an “unstructured” neural architecture, because it leverages smart engineering solutions. We learn its parameters by reinforcement learning as follows: simulate a problem, apply your neural augmented solver (a.k.a. policy), then compute the goodness of your solution (your reward), and if the solution was good, reinforce the moves that led to it (and penalize the bad moves). Rinse and repeat. The result of this is not necessarily a policy that is always better than the dedicated classical solvers for a given problem. However, the learned policy can be executed quickly, is robust to a changing environment, and can naturally handle uncertainty.
In summary, combinatorial optimization problems are ubiquitous. By building on decades of engineering and leveraging recent progress in machine learning, we can build hybrid systems that combine the best of both worlds: highly accurate, adaptive, and robust systems that learn to plan like no human can.
Dr. Max Welling
Vice President, Technology, Qualcomm